数学ができないのは「頭が悪いから」ではない！つらさを解決する勉強法
数学ができないと、数学の成績が伸びません。連動して理科が伸び悩むこともあり、決して看過できない問題です。 しかし「数学ができない・つらい」「できれば数学をやりたくない」という気持ちもあり、いったいどうすれば良いのかと悩んでいるのではないでしょうか。 この記事では自身も数学が苦手だった筆者が、数学ができるようになった今だからこそわかる「数学とは」を解説します。数学ができない理由やできるようになる勉強法、一歩踏み出す勇気がもらえる話など満載です。 ぜひ最後まで読んでみてください。 あなたの数学に少しでも光が差したら、克服への道を一緒に歩み始めましょう。
「数学ができない ＝ 頭が悪い」が成り立たない理由
よく「自分は頭が悪いから、数学ができない」「勉強ができないのは、頭が悪いせいだ」という人がいます。
しかし「数学ができないこと」と「頭の良し悪し」はイコールの関係にはありません。そもそも頭が良い・悪いとは？そして数学に必要な力とは？順番に考えていきましょう。
そもそも「頭がよい」「頭が悪い」とは？
「頭が良い」「頭が悪い」とは、なんとも抽象的なことばです。場面や状況によっても、さまざまな意味合いを含み持つでしょう。 学校の勉強という場面に限って考えると、一般的には「成績が良い・テストの点数が良い」人が頭が良いとされるようです。 しかし偏差値35から2浪人を経て東京大学に合格した著作家の西岡壱誠氏は、「頭が良い」を次のように表現しています。- 頭が良い人とは、学びにつながる「目」を持っている人
- 日常生活のさまざまなところから学ぼうとする人
- 日頃から「なぜ？」と疑問を持ち続けている人
数学には勘もセンスも必要ない
よく「数学にはセンスが必要だから」「あの人はひらめきがあるから、勘がいいから数学ができるんだ」といった言葉も耳にします。 しかし、学校で学び受験で使う数学に限っていえば、勘もセンスも必要ありません。 受験数学を突破するために必要なのは、暗記力と読解力、そして少しの論理力です。 テストに出題される数学の問題は、どれも初めて見た問題のような気がします。しかし、問題に含まれる情報を精査し並べてみると、解いたことのある問題に行きつきます。組み合わせや文章表現の仕方を変えて、あたかも初見であるかのように見せているだけということも多いのです。 必要な知識を正しく暗記し、問題文を読解して必要な情報を抽出し、論理が通るように使っていけば、ほとんどの数学の問題は解けてしまいます。 さらに公立高校入試や大学入学共通テストでは「教科書内容を逸脱する問題を出してはいけない」と定められています。そのため、教科書で習った以上の知識を必要とする難問・奇問は出題されません（私立高校入試や大学個別試験は、難問・奇問が出る場合もあります）。 受験数学は、センスや勘がなくても努力できちんと突破できます。数学に必要なのは読解力と論理力
「数学に必要なのは、暗記力と読解力、そして論理力」と前述しました。さて暗記力は暗記した知識量ですから置いておくとしまして、読解力と論理力とはどのような力でしょうか？ 数学における読解力とは、問題文から必要な情報を正しく読み取る力を指します。長いながい文章題も、解くために必要な情報だけに絞ってみるとごくわずかだった、というのはよくあることです。ただし、小説を読む姿勢とは異なります。自分で勝手に想像を膨らませてはいけません。 書いてあることを、書いてある通りに間違いなく抜き出す力、だと考えてください。 論理力とは、物事や条件を筋道を立てて組み立て考える力です。「こうだから、こうなる」と論理を通せる考え方を指します。問題文が読み取れても、論理力がないと抽出した情報をどのように処理すれば良いかわからなくなってしまいます。 「Aの条件とBの条件を用いて、Cを導く（ただしDは例外）」と筋道を立てて答えを導くときに必要になるのが、論理力です。 読解力と論理力は、新しい学習指導要領でも重視されています。数学が理解できない原因は？
「数学が理解できない」とお悩みの場合、いくつかその原因が考えられます。原因を理解することで、苦手の解決に近づけるかもしれません。
ここでは、数学が理解できない原因として考えられるものを紹介しますので、自分の状況にあてはまるものがないかを考えてみましょう。
勉強の仕方が自分に合っていない
「数学の勉強に時間をかけているのに、なかなか成績につながらない」という人は、勉強の仕方が自分に合っていないのかもしれません。 数学の成績を上げるためには、正しい勉強法・自分に合った勉強法で実力を身につけていくことが必要です。 「おすすめの勉強法」「やってはいけない勉強法」については、後ほど詳しく紹介するので、勉強法に自信がない人はそちらも合わせて参考にしてください。勉強時間が足りていない
数学が理解できない原因として、そもそも勉強時間が足りていないことも考えられます。 数学は他教科に比べて暗記する事項がそれほど多くないと思われがちで、勉強が後回しになることも少なくありません。 しかし数学も公式や定理を理解したり、できるまで演習を重ねたりと、しっかりと時間をかけて勉強する必要のある教科です。 勉強時間が確保できていないと感じる人は、まずは数学と向き合う時間を増やすことから始めましょう。授業の予習や復習の時間を増やすだけでも、理解度を高めることができますよ。苦手な単元やつまずいている場所がわからない
数学に対して苦手意識があるものの「自分が苦手とする単元や、つまずいている場所が具体的にわからない」ということはありませんか？ 実は「どこがわからないか」が理解できていないことが原因で、数学を勉強してもなかなか身につかない人も多いです。 特に数学は、小学校の算数・中学校の数学・高校の数学と知識を積み重ねていく形で内容が進んでいきます。 たとえば、高校で詳しく学習する「二次関数」がわからない場合は、中学生で習う「一次関数」から理解できていないかもしれません。 高校生でも場合によっては、中学校あるいは小学校までさかのぼって復習が必要な場合もあります。そのためまずは、自分が苦手な単元や、つまずいているポイントを見つけることが重要です。 逆に、自分がどこでつまずいているかを正しく把握できれば、その単元を重点的に学ぶことで苦手を克服できるでしょう。数字や計算などに苦手意識がある
中には「どうしても数字の扱いや計算が苦手」という人もいるでしょう。 数学においてはどの単元においても、基本的には数字や計算から逃れることができません。 数字や計算が苦手な人は、扱いやすい問題を使って徐々に慣れていきましょう。 たとえば高校生の場合、まずは中学生の計算問題から復習していくのがおすすめです。 解ける問題が増えていけば自信につながり、少しずつ苦手を克服していけるでしょう。学校の授業スピードについていけていない
通っている学校によっては、授業スピードがとても早い場合もあります。 一つ理解できなかった部分があるだけで、その先の授業も理解できなくなることも十分あり得るでしょう。 日々予習・復習をすることはもちろん、わからない・ついていけない部分があれば、その都度先生に確認したり、質問したりすることも大切です。高校数学はなぜ難しい？
特に「高校生になって数学が苦手になった」「高校に入ってますます数学がわからなくなった」という人は多いです。
高校数学は難しいと言われますが、実際はどんな点に難しさがあるのでしょうか。
ここでは高校数学の難しさに迫っていきましょう。
中学校での学習内容が前提となっている
まず、中学校の学習内容を理解していることが前提となっている点が、高校数学の難しいところです。 高校では、中学校で学習したことを土台にしながら、新たな内容を学んでいきます。 土台に足りない部分があれば、その上に知識を積み重ねることは難しいです。 特に中学時代に数学に苦手意識を抱えていた人や、数学の勉強を後回しにしていた人は、さらに高校数学を難しく感じることでしょう。内容がさらに複雑になる
高校数学は、中学校に比べて内容がさらに複雑になります。 「集合」「虚数」「数列」「微分・積分」「数学的帰納法」「ベクトル」など、新たに登場する定理や概念も多いです。 中学まで数学が好きだったという人も、高校になってつまずいてしまう場合もあります。 大学受験で数学を使うことを考えている人は特に、粘り強く数学と向き合うことが求められるでしょう。覚える公式や定理が増える
内容が複雑になれば、その分覚えなければならない公式や定理も増えることになります。 中には定理や「なぜそうなるか」を理解することが難しいものや、公式自体が複雑なものも登場する点が、難易度が一気に上がるポイントです。 1年生のうちからコツコツと知識を積み重ねておくことが、大学受験の数学で苦労しないコツの一つと言えるでしょう。学校では「数学ができないとつらい」は事実
「数学にはセンスも勘も不要、読解力と論理力で解けるようになる」といわれても、現実問題として数学ができないとさまざまな「つらさ」に直面します。
◎ 数学ができないと……
- 授業がつまらなくなる
- 成績（内申点）が低くなる
- 進路選択の幅が狭まる
数学が理解できない現状を克服する方法
ではここからは、数学が理解できない現状を克服する方法を詳しく紹介していきます。
すぐに始められるものばかりなので、明日からの数学の勉強でぜひ取り組んでみてください。
まずは勉強時間を確保
「そもそも数学に時間を割けていない」という人は、まずは勉強時間を確保することから始めましょう。 何を勉強すればいいかわからない人は、以下2つの勉強を日常的に行うのがおすすめです。- 学校授業の予習・復習 →教科書を読み、例題や基本問題を解く
- 数学の単元を網羅した問題集の演習 →「チャート式」などの問題集を進める
自己分析して苦手を見つける
「どこでつまずいているかわからない」という人は、以下の方法で自己分析をしてつまずきポイントを見つけることが必要です。- 数学の単元を網羅した問題集を解き進める
- わからない問題があれば、単元をたどって復習する
- 必要に応じて中学内容も復習する
正しい学習ステップで勉強する
数学を勉強する際は、正しい学習ステップを踏んで勉強することも大切です。 最初から問題集を解き始めたり、よくわかっていないままで次の単元に進んだりしていても、なかなか実力が身につきません。 各単元の内容をしっかりと理解した上で問題演習に進んでいけるよう、以下のようなステップで勉強を進めるのがおすすめです。- 教科書で公式や基本問題を確認する
- 問題集の基本問題を解く
- 問題集の発展問題を解く
- 定期的に復習する
繰り返し復習する
どれだけ勉強が得意な人でも、一度学習しただけでその後も完璧に問題が解けるという人は少ないです。 人間の脳は、一旦覚えたことも時間が経つと忘れてしまう構造になっています。 つまり、勉強したことを自分の実力として定着させるためには、何度も復習することが欠かせません。 数学に関しても、一度学習して理解した内容を繰り返し復習することで、少しずつ大切な知識として頭に定着させることができます。 そのため、問題集を何周も繰り返したり、わからなかった問題を定期的に解き直したりして、繰り返し復習することも大切にしましょう。数学にやり直しは必要！復習のメリット
数学にやり直しは必要です。わからなくなったとき、不安を感じたときに必要な箇所まで戻ってやり直すと、以降の学習が劇的に楽になります。
数学のやり直しによって得られるメリットは、次の3つです。
- 正しく理解できる
- つながりのある他の単元の理解も深まる
- 不安が解消され、自信が持てる
数学のやり直し学習・基本の3ステップ
数学のやり直し学習を効率的に進める手順を、3つに分けて解説します。この3ステップは、中高生に共通です。
「やり直しが必要だと思うが、何から手を付ければよいかわからない」人は、ぜひ参考にしてください。
step1. 苦手単元、不安な単元を見つける
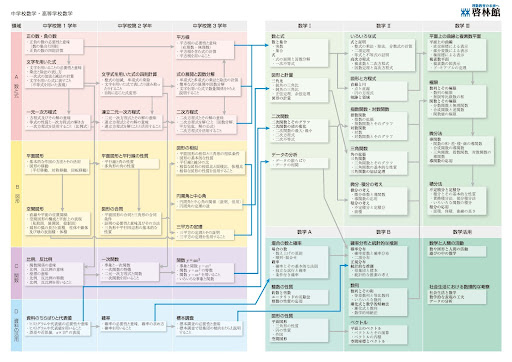
はじめに、苦手な単元や不安な単元を見つけましょう。これまでに学んだ数学の全体像を俯瞰できる資料があると便利です。 教科書や参考書の目次のほか、教科書会社が公開している「単元関連表」も活用できます。下の画像は、教科書発行会社である「啓林館」による数学の単元関連表です。 画像1枚目の右側と画像2枚目の左側に中学数学が、画像2枚目の右側に高校数学が掲載されています。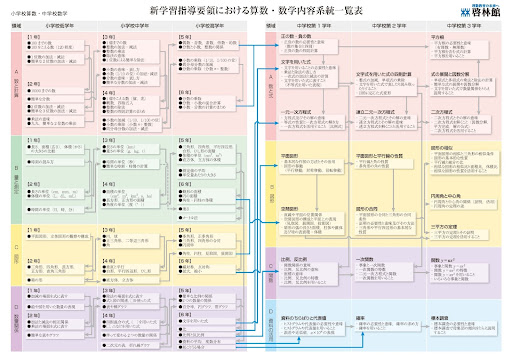
引用：新学習指導要領における算数・数学内容系統一覧表｜啓林館
数学のやり直し学習を進める際は、「以前習った関連する単元」の復習が必要になる場合があります。関連表を使うと、苦手単元の土台になる単元が一目瞭然で学習計画が立てやすくなります。
step2. 基本から丁寧に解説する参考書に取り組む
苦手・不安な単元が見つかったら、基本からわかりやすく解説する参考書を片手に復習をはじめましょう。 苦手な単元は、教科書の解説だけを読んでもよくわからないことが多いものです。教科書の解説は基本に忠実で、定理・定義を正しく述べているためです。 「なぜそうなるのか」「どうしてそう考えるのか」といった考え方の部分を詳しく解説している参考書を探してみてください。講義形式（対話式）でまとまっている参考書は、解説が平易で独学に向いています。◎ 中学数学｜対話形式の参考書
『やさしい中学数学 改訂版』（学研プラス）
◎ 高校数学｜対話形式の参考書
『大学入学共通テスト 数学I・Aの点数が面白いほどとれる本』（KADOKAWA）
※ 数II・B版もあります
step3. 問題演習は短期間で3周する
講義形式の参考書で基本を理解しつつ、問題演習も進めましょう。 問題演習は参考書に付属の問題か、使いやすい問題集を用意します。基本レベルで解説が詳しいものを選んでください。 ポイントは「短期間で3周する」ことです。周回ごとに異なる目的があり、一通りの学習を完了させられるのが「3周」だからです。 ◎ 問題集を3周する目的- 1週目：理解した知識を試し、問題ごとの「できる／できない」を明確にする
- 2週目：1週目でできなかった問題をできるようにする
- 3週目：通してとき、抜け漏れがないか再チェックする
高校受験生向け・数学のやり直し学習のコツ
高校受験を控えた中学生が、数学のやり直し学習を進めるコツを解説します。高校入試では難問・奇問は出されないため、基本を重視した学習が数学の得点を底上げしてくれます。
3年分の定期テストから苦手を見つけよう
はじめに苦手分野・単元を見つけましょう。模試の成績表からも苦手を見つけられますが、おすすめは3年間の定期テストを振り返ることです。 定期テストを順に見返しながら「苦手だと感じた問題」「解ける実感がなかった問題」をピックアップしてください。抽出された問題を単元ごとに分類し、もっとも多かった単元が最優先で克服しないといけない苦手単元です。高校入試での出題傾向も把握しよう
苦手単元の発見と同時進行で、高校入試の出題傾向もチェックしてみてください。 高校入試の問題は、都道府県ごとに傾向があります。「毎年必ず出る単元」「ほんとど出ない単元」を区別しましょう。 苦手単元が頻出なら優先的に克服する必要がありますし、ほとんど出ない単元なら後回しにしても良いかもしれません。学校の問題集で基本をしっかりマスターしよう
中学生のやり直し学習におすすめの教材は、学校で配布された問題集です。収録されている問題は基本をしっかり網羅しており、無理なく理解できる構成になっています。 学校問題集を仕上げたら、高校入試向けの問題集に取り組みましょう。全国の高校入試問題を収録した問題集もおすすめです。
『2023年受験用 全国高校入試問題正解 数学』（旺文社）
近年は学習指導要領の改訂にともない、新傾向と呼ばれる問題も増えています。新傾向の問題はまだ数が多くないため、他県の入試問題を参考に今年の入試問題を作成するケースもあります。
自県の過去問だけでなく、他県の問題にチャレンジしておくとより実戦的な力が身に付きます。
国立文系受験生向け・数学のやり直し学習のコツ
国立文系を目指す受験生は、共通テスト対策が学習の中心になります。共通テストでボーダーラインを超える点数を取れるよう、しっかり準備していきましょう。
国立文系受験生向けに、数学のやり直し学習のコツを解説します。
模試を分析し苦手単元を見つけよう
「数学は全体的に苦手だ」という受験生もいるかもしれませんが、まずは苦手単元を整理する作業からはじめます。 利用するのは模試の成績表です。得点率や評価、ヒストグラムを参考に「安定的に得点できていない単元」「突出して得点できていない単元」を見つけましょう。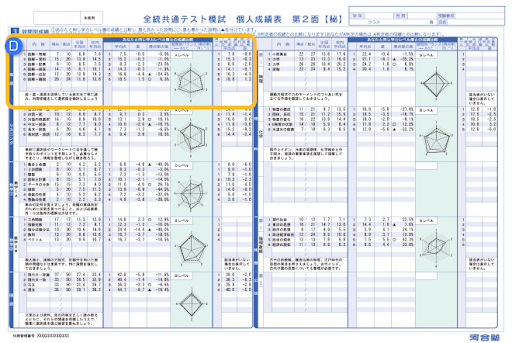
引用：個人成績 | 返却資料・成績確認方法 | 全統模試案内 | 大学受験の予備校・塾 河合塾
画像は、河合塾が実施している「全統模試」成績表の裏面です。裏面には科目ごと・設問ごとの成績が記載されています。
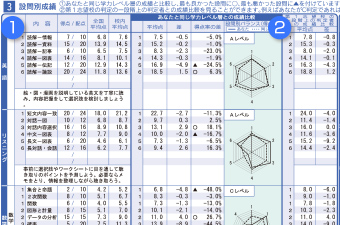引用：個人成績 | 返却資料・成績確認方法 | 全統模試案内 | 大学受験の予備校・塾 河合塾
設問別の成績を見ると、とくに補強が必要な分野がわかります。平均点と比べて得点が低い分野や、同じ学力層の仲間より出来ばえが悪かった分野も把握しましょう。
チャート式（黄色）を学習の中心に据えよう
苦手分野が明確になったら、黄色のチャート式などを使い復習を進めます。 共通テストのみで数学が必要な国立大文系受験生の場合、あまり難しすぎる参考書は不要です。それよりも基本を丁寧に解説し、必要な問題を網羅している参考書を選んでください。 この段階では、共通テストの問題形式は意識しなくて大丈夫です。はじめから終わりまで自分の力で記述できるように、過程を飛ばさず解けるよう練習しましょう。共通テスト形式の問題に慣れよう
復習がある程度進んだら、徐々に共通テスト形式の問題に合わせていきます。 共通テストの数学は「時間内に」「正確に」解ききる力が要求されます。また問題文や条件解説が長く、読解力が必要な問題も増えてきました。時間を意識し、要点を押さえて解き進められるよう練習してみてください。 共通テストの過去問はまだ数年分しかストックがないため、予想問題集やセンター試験の過去問を使うのもおすすめです。理系大学受験生向け・数学のやり直し学習のコツ
ほとんどの理系大学受験生は、2次試験・大学個別試験でも数学を使います。国立大学なら記述式問題が、私立大学は見たことがないタイプの問題が出されることを踏まえても、基本をしっかり押さえ発展的な問題に対応できる力をつけることが大切です。
理系大学受験生向けの数学のやり直し学習のコツを解説します。
足を引っ張っている単元を見つけよう
数学の得点が伸び悩んでいる単元を見つけましょう。「模試で毎回得点できない単元」「出題されると気分が滅入る単元」などが該当します。 理系受験生は共通テストで数学I･AとII･Bを、2次試験・個別試験で数学IIIを使います。マーク模試（共通テスト模試）では数学II･Bまでしか範囲にならないため、記述模試の成績表もチェックしてください。チャート式（青色）でサクッと復習しよう
理系受験生の数学やり直し学習におすすめなのは、青色のチャート式です。
『チャート式基礎からの数学III』（数研出版）
青チャートは教科書レベルの基本問題から、入試レベルの発展問題までを収録しています。理系の受験生がかならずマスターしておきたい問題ばかりが並んでいるため、これ1冊で入試対策まで万全です。
またすべての例題は、アプリで解説動画を視聴できます。書籍の解説だけではわからない問題だけ動画を見るといった使い方もできるため、時間を効率良く使えます。
参考：解説動画アプリ「数研Library」
2次試験対策を学習の中心に据えよう
理系受験生の場合、やり直し学習を進めるあいだも2次試験・個別試験が最終目標だということを忘れないでください。 共通テストと2次試験・個別試験のあいだには、大きな壁があります。 ◎ 共通テストと2次試験・個別試験の壁- 問題の難度
- 出題範囲
- 解答にかかる時間
- 必要な理解度、習熟度
数学ができない人がやるべき勉強法
数学ができない人が、一念発起して数学を克服したいと思ったら、何から手を付ければ良いのでしょうか。
スモールステップで無理なく、徐々に数学がわかるようになる学習法を解説します。
基礎基本を徹底的にやり直す
まずは基礎基本からです。教科書レベルの内容を、しっかり理解しましょう。教科書に載っている公式や定理・定義を正しく理解します。 このとき、暗記に走らないよう気を付けてください。数学ができるようになるために大切なのは「なぜそうなるのか」という理解の部分です。 教科書だけで理解できない場合は、教科書ガイドや映像授業を利用しましょう。 算数までさかのぼっての復習も効果的です。小学5・6年生の算数は数学に直結する内容を数多く扱っています。あらためて算数を勉強してみると当時より理解しやすく、長年の疑問が解決する可能性もあります。 数学嫌いが算数に起因している人には、効果的な学習法です。与えられた条件と求める結果、手順を整理する
数学はどの単元も、基本となる解き方が存在します。教科書の例題や練習問題で扱う問題と解法が該当します。 はじめは例題を見ながら、徐々に見る頻度を減らしながら、基本の解き方をマスターしましょう。 この時、注意して身につけたい点は次の3つです。- 与えられた条件は何か
- 求める結果は何か
- 解法の手順はどのようか
数学言葉を「翻訳する」練習をする
数学は、独特の言い回しで書かれます。解ける状態にするために、必要な情報を抜き出しつつ（不要な情報を排除する）平易な表現に書き換える練習をしてみましょう。 たとえば中2で学ぶ「一次関数」の文章題を例にして解説します。タテの長さが3cm、横の長さが4cmの長方形ABCDの周上を、点Pは毎秒1cmの速さで、AからB、Cを通ってDまで移動します。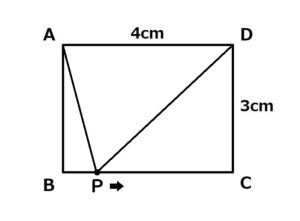
PがAを出発してからx秒後の△APDの面積をy cm²とするとき、yはxの変化にともなってどう変化するのか説明しなさい。 |
| 問題文の表現 | 翻訳後 |
|---|---|
| 点Pは毎秒1cmの速さで | 1秒後には1cm、2秒後には2cm…、x秒後にはxcm進んだ位置にある |
| △APDの面積 y cm² | y＝1/2×底辺（AD）×高さ→ y＝2×高さ ※ 高さはA→Bでは xcm、B→Cでは3cm（一定）、C→DではAB（3cm）＋BC（4cm）＋CD（3cm）－x＝10－x cm |
| yはxの変化にともなってどう変化するのか | 「ともなって変わる数」＝関数比例か、一次関数か、二次関数のいずれか。 |
自分に合うレベルの教材を繰り返す
中高生の数学は、反復学習が成否を分けます。自分に合うレベルの教材を見つけ、最低でも3回は繰り返してみてください。- 1回目は、自分の理解度と実力をチェックするために。
- 2回目は、1回目でできなかった問題をできるようにするために。
- 3回目は、すべての問題を完璧にできるようにするために。
自分に合う家庭教師を探す
数学ができない・嫌いな中高生が数学の勉強に取り組む際は、塾より家庭教師がおすすめです。家庭教師なら自宅で受講できるため、周りからの視線を気にせず勉強に集中できます。また塾講師には大学生のアルバイト講師が多いのですが、家庭教師は本当に力のある良い先生がいる可能性があります。 もし近くに良い先生がいない場合は、オンラインでの受講も検討してみましょう。オンライン家庭教師なら、全国各地にいる先生と出会えます。数学が理解できないときにやってはいけない勉強法
数学が理解できないとお悩みの人に、おすすめできない勉強法もあります。
「勉強しているのに成績が上がらない」という人は、勉強の仕方が合っていないかもしれません。
数学が得意になるために、以下のような勉強法は避けるようにしましょう。
解答を丸写しして満足する
数学でわからない問題があったら、答え合わせで解答を書き写すことになると思います。 解答を丸写しし、そこで終わってしまってもその問題が解ける状態にはなっていません。 最も大切なのはそこから「なぜこの解き方になるのか」「自分はどこでつまずいたのか」を明確にして、解き直しや復習を行うことです。 解答を丸写しして満足せず、必ずその後の復習に時間を使うようにしましょう。すべて丸暗記しようとする
間違えた問題の解き直しや復習の際に気をつけたいのが、模範解答をすべて丸暗記しようとすることです。 解き方を理解することなく、丸暗記するだけでは、出題内容が少し変わっただけでも対処できなくなってしまいます。 数学が得意になるためには「解き方を理解する→自分で解けるようになること」が必要です。 丸暗記に時間をかけても、問題によってはどうしても対応できないため、問題集などを演習する際は注意しましょう。難しい問題に時間をかけすぎる
わからない問題や難しい問題に遭遇すると、どうしても時間をかけて考えてしまいがちです。 一つ一つに時間をかけすぎていると、勉強が効率よく進まない状態となってしまいます。 しばらく問題と向き合ってもわからない場合は、早めに先生に質問するのがおすすめです。 解き方を理解させてもらったら、それを自力で使いこなせるまで練習することに時間を費やしてみましょう。 特に受験問題の中には、高難度の問題もあります。こうした問題に時間をかけすぎてしまうと、点数につながりやすい問題が疎かになってしまうかもしれません。- まずは基本問題からできる問題を増やす
- 一定時間考えてわからない問題は先生に質問する
- 高難度の問題に時間をかけすぎない
数学ができない人におすすめの教材
数学ができない・嫌いな中高生が「それでも数学を頑張りたい」と思い、勉強する際におすすめの教材を3つ紹介します。それぞれの特徴やメリットをまとめましたので、自分に合いそうなものを試してみてください。
参考書・問題集
もっとも手軽で費用も抑えられるのが、参考書や問題集です。学び直し用のテキストや講義形式で解説されたテキストもあり、独学でもわかりやすい解説を使いながら勉強できます。 店頭で実際に手に取って探せるため、自分に合うものを選びやすい点もメリットです。 デメリットは、わからないところがあったときに困りやすい点でしょう。学校や塾の先生、家庭教師など、質問できる相手を見つけておくことが大切です。タブレット教材
あらかじめタブレットに教材を収録しておき、自分のペースに合わせて学習を進められるタブレット学習も、数学のやり直しに向いています。タブレットに搭載されたAIが苦手な問題を分析し、自動的に反復学習させてくれるためです。 ゲームやお楽しみ要素もあり、飽きずに続けやすい点もメリットです。 ただし、参考書や問題集同様に「質問できない」点がネックになります。タブレット教材のなかにはオプションとしてオンラインで質問できるサービスを用意しているところもあるため、利用を検討しても良いでしょう。映像授業
映像授業は、実力派講師のわかりやすい解説授業を視聴して学ぶスタイルの教育サービスです。録画された授業がストックされており、レベルや目的に合わせて豊富なラインナップから選べる点がメリットです。受講費用も抑えられます。 ただし授業をしている講師に質問はできません。質問がある場合は、オプションの個別指導コースに申し込む必要があります。独学・先取りのためのおすすめ参考書・問題集
やさしい高校数学シリーズ
はじめに紹介するのは学研が出版しているやさしい高校数学（1A/2B/3）です。この参考書は未習分野を初めてやるときに役立つものになります。内容としては教科書よりも詳しく、そしてわかりやすい説明が語り口調で記されています。とても分厚い本ですが、文章でギッチリ埋まっているわけではなく文と文の間にすき間があるので読むときに負担が少なく続けやすいかと思います。 また解説が詳しいため先取りだけではなくあまりわからなかった箇所を復習するためにも重宝する参考書となっています。また学校の定期試験レベルの演習問題もついているためある程度の力をつけられることでしょう。チャート式基礎からの数学シリーズ
続いて紹介するのは数研出版が出しているチャート式基礎からの数学（1A/2B/3）、通称青チャートです。こちらの参考書は学校で教材として使われることも多く、長年にわたって愛されてきた参考書なので買ってみてまず間違いはありません。 先ほど紹介したやさしい高校数学シリーズと比べるとこちらは演習書なので公式などの説明が端折り気味ですが、数学に苦手意識がそれほどないのであれば青チャートから始めても問題はないでしょう。演習を積んでいく中で理解を深めたい人には最適な問題集だと思います。一対一対応の演習シリーズ
次に紹介するのは東京出版が出している一対一対応の演習（1/A/2/B/3）です。この問題集は青チャートの標準問題を一通りこなしたあとにやるべき問題集で、基本から応用への橋渡し、テスト勉強から受験勉強への橋渡しを担ってくれる問題集です。一つの例題に詳細な解説が付され、さらに下に練習問題として類題が一問掲載されています。 青チャートに載っている問題や定期テストに出てくる問題は、数学の公式や仕組みの理解、計算能力の確認がメインでしたが、この問題集では受験に必要な思考力、応用力を身に付けることが出来ます。一問につき一つの類題なので一見問題数はそう多くないように思えますが、今までに比べ難易度が高いのと、数学1、A、2、Bで一冊ずつ、数学3で2冊の合計6冊と数が多いので意外とこなすのには時間がかかるので注意しましょう。【基礎レベル】おすすめの参考書・問題集
合格る計算シリーズ
はじめに紹介するのは合格る計算（1A2B/3）です。この問題集は題名の通り計算を主軸においた問題集です。もっと実践的な問題集をやりたい！という気持ちはわかりますが、難しい問題になればなるほど計算に手間取る暇がなくなるので計算力を上げるためにもやっておきたい一冊です。頭のいい人がどのような手順で計算をしているか、いかに計算を簡略化するか、そのノウハウが丁寧に記されています。計算に苦手意識がある人や計算ミスが多い人はやってみることをおすすめします。基礎問題精講シリーズ
次に紹介するのは旺文社が出版している基礎問題精講（1A/2B/3）です。有名な数学の問題集の一つで大変バランスの良い問題集です。内容としては例題と演習問題がそれぞれ130題前後ずつ用意されておりそれぞれに細かな解説が付されています。先ほど紹介した青チャートと問題の難易度は変わらないため独学としても使えるほか、青チャートに比べ問題数が半分以下であるため取り組みやすいという特徴があります。長年多くの受験生に使われてきた問題集であるためやってみて後悔することはないでしょう。【実践レベル】おすすめの参考書・問題集
新数学スタンダード演習
まず紹介するのは東京出版が出している新数学スタンダード演習です。この問題集は受験スタンダードレベル～やや難レベルの問題を分野別に掲載しています。中堅私大・国立大～難関私大の問題が多く、さらに演習価値の高い問題が多いことが特徴です。 この問題集を使うことで得られることとしては入試問題に対するアプローチの仕方や定石の習得があります。計算の仕方や解説の意味は理解できるけど自分ではその解答を再現できない、最初の一手が分からないといった悩みを持つ受験生はこの問題集をやることでその悩みが解決されることでしょう。理系数学の良問プラチカシリーズ
続いて紹介するのは河合出版の理系数学の良問プラチカ（1A2B/3）です。こちらの問題集のレベルとしは新数学スタンダード演習と同程度であり、どちらか一方を選択して取り組んでみるのが良いでしょう。二つの問題集の違いですが、こちらの問題集は新数学スタンダード演習に比べて問題数が少なく、難問・奇問が少ないということが挙げられます。 変にひねった問題はなるべく避けて他の問題にも応用できる解法が紹介されています。奇を衒った問題がないのでやっていて苦痛に感じることが少ないため進めていきやすいと思います。【難関～超難関レベル】おすすめの参考書・問題集
やさしい理系数学
まず紹介するのは河合出版の出しているやさしい理系数学です。この問題集は「やさしくない」ことで有名で普通に難しいです。レベルとしては難関私大・中堅国立大～難関国立大レベルであり、分野別に問題が掲載されています。また、別解が豊富に掲載されていることも特徴の一つで、一つの問題を別の角度から見ることが出来るので数学的な視野を広げることが可能です。 注意点としてこの問題集は解答が複数ある一方でその解説はあまり載っていません。数式と言葉だけで理解出来る人、つまりある程度数学を理解している人でないとつまずいてしまう可能性もあります。この点にだけは注意しましょう。上級問題精講
次に紹介するのは旺文社が出版している上級問題精講（1A2B/3）です。先ほど紹介した基礎問題精講と標準問題精講とこちらの上級問題精講が同シリーズですが、この問題集は難易度が飛びぬけて高いです。やさしい理系数学よりも一回り難易度が高く、難関国立大の問題が多くを占めています。基本的な構成は基礎問題精講と同じで例題一題に付き一つの類題が示されていて演習がしやすい形になっています。この問題集を完璧にこなすことが出来れば国立大医学部や東大・京大の数学でも物怖じせずに立ち向かうことが出来るでしょう。入試数学の掌握シリーズ
最後に紹介するのはエール出版が出している入試数学の掌握（赤/青/緑）です。この参考書は私が今まで見てきた中で最高難度の参考書です。この参考書は章立ても特徴的で、単元ごとではなく、通過領域・全称命題などテーマ別に分けられています。問題が難しいからと言って決して理解が難しいのかというとそうではなく、非常に丁寧な解説がついています。 問題として取り上げられているのは東大・京大・一橋大など最高峰の大学が多数を占めており、この参考書の対象者も東京一工、医学部志望に限られるでしょう。この参考書は三冊でシリーズとなっており中でも青色の表紙である各論錬磨編には通過領域の詳細な解説が掲載されており、通過領域に苦手意識のある人にはいい練習の機会となると思います。数学ができないときに頼りたい！オンライン家庭教師の魅力
「自分に合った解説をしてほしい」「わからないことはその場で解決したい」と考える中高生には、オンライン家庭教師がおすすめです。
オンライン家庭教師とはオンラインで指導を受ける家庭教師を指し、自宅にいながらマンツーマンで授業を受けられます。周りの目を気にせず、自分の勉強だけに没頭できる点がメリットです。